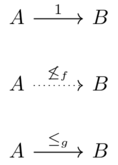Changing the base of enrichment

Induced V-categories from monoidal monotones(2)

Let \(\mathcal{V}\xrightarrow{f}\mathcal{W}\) be a monoidal monotone map. Given a \(\mathcal{V}\) category, called \(\mathcal{C}\), one can construct an associated \(\mathcal{W}\) category, let’s call it \(\mathcal{C}_f\)

Proof(1)

  • Take the same objects: \(Ob(\mathcal{C}_f):=Ob(\mathcal{C})\)

  • \(\mathcal{C}_f(a,b) := f(\mathcal{C}(a,b))\)

  • Check this obeys the definition of an enriched category:

    • Condition on the monoidal unit:

      1. \(I_W \leq f(I_V)\) — from the first condition of a monoidal monotone map.

      2. \(\forall c \in Ob(\mathcal{C}): I_V \leq \mathcal{C}(c,c)\) — first condition of an enriched category, which \(\mathcal{C}\) is

      3. \(\forall c \in Ob(\mathcal{C}):f(I_V) \leq f(\mathcal{C}(c,c))\) — monotone map property

      4. \(\forall c \in Ob(\mathcal{C}):f(I_V) \leq \mathcal{C}_f(c,c)\) — definition of \(\mathcal{C}_f\)

      5. \(\forall c \in Ob(C_f): I_W \leq C_f(c,c)\) — transitivity, using 1 and 4, noting \(Ob(\mathcal{C})=Ob(\mathcal{C}_f)\)

    • Condition on monoidal product:

      1. \(\mathcal{C}_f(c,d) \otimes_W \mathcal{C}_f(d,e) = f(\mathcal{C}(c,d)) \otimes_W f(\mathcal{C}(d,e))\) — definition of \(\mathcal{C}_f\)

      2. \(f(\mathcal{C}(c,d)) \otimes_W f(\mathcal{C}(d,e)) \leq f(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e))\) — second condition of a monoidal monotone map

      3. \(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e) \leq \mathcal{C}(c,e)\) — Second condition of an enriched category

      4. \(f(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e)) \leq f(\mathcal{C}(c,e)\) — monotone map property

      5. \(f(\mathcal{C}(c,d) \otimes_V \mathcal{C}(d,e)) \leq \mathcal{C}_f(c,e)\) — definition of \(\mathcal{C}_f\)

      6. \(\mathcal{C}_f(c,d) \otimes_W \mathcal{C}_f(d,e) \leq \mathcal{C}_f(c,e)\) — transitivity, 1,2 and 5

Linked by

Metric space to preorder(1)

Linked by

Exercise 2-67(2)

Recall the “regions of the world” Hausdorff metric space We learned that a metric space can be converted into a preorder by a particular monoidal monotone map. How would you interpret the resulting preorder?

Solution(1)

The edges in the preorder represent the \(\subseteq\) relation. For Boston, US, and Spain, it would look like this (with implicit self-edges):

Exercise 2-68(2)

Find a different monoidal monotone map \(\mathbf{Cost}\xrightarrow{g}\mathbf{Bool}\) from the one in Example 2.65. Using the construction from Proposition 2.64, convert a Lawvere metric space into two different preorders. Find a metric space for which this happens.NOCARD

Solution(1)